Page 22 - การจัดทำค่ามาตรฐานธาตุอาหารพืชในชาน้ำมันเพื่อใช้เป็นค่าวินิจฉัยสำหรับให้คำแนะนำปุ๋ย Preparation of Standard Plant Nutrients in Camellia oleifera Able. for Use as Diagnostic for Fertilizer Recommendations.
P. 22
ห้องสมุดกรมพัฒนาที่ดิน
12
3.3 การใช้สมการพหุนามก้าลังสอง (quadratic equations method)
2
การใช้สมการพหุนามก้าลังสอง (y = ax + bx +c) จัดท้าค่ามาตรฐานธาตุอาหารพืช เป็น
วิธีที่คล้ายกับการใช้วิธีเส้นขอบเขต เพียงแต่วิธีเส้นขอบเขตใช้เส้นแนวโน้มสองเส้นในการวิเคราะห์
ความสัมพันธ์ของข้อมูล ในขณะที่การใช้สมการพหุนามก้าลังสองใช้เส้นแนวโน้มเพียงเส้นเดียว จึงช่วยลด
ความยุ่งยากในการประมวลผล การใช้วิธีนี จะได้เส้นแนวโน้ม ที่มีลักษณะเป็นเส้นโค้งรูประฆังคว่้า โดยอาศัย
หลักการตอบสนองของพืชต่อความเข้มข้นของธาตุอาหารเช่นเดียวกับการใช้วิธีเส้นขอบเขต คือ ในช่วงแรก
ความต้องการธาตุอาหารพืชจะเพิ่มขึ นจนถึงระดับที่พืชมีการเจริญเติบโต หรือให้ผลผลิตสูงสุด แต่หลังจากนั น
ผลผลิต หรือการเจริญเติบโตจะลดลง หากความเข้มข้นธาตุอาหารยังคงเพิ่มขึ นอีก จากการใช้สมการพหุนาม
ก้าลังสองก้าหนดความเข้มข้นของก้ามะถันที่เหมาะสมในใบยางพาราระยะก่อนเปิดกรีด พบว่า ความสัมพันธ์
ระหว่างการเจริญเติบโตของต้นยางพารากับระดับก้ามะถันในใบเป็นไปในลักษณะเส้นโค้งรูประฆังคว่้า
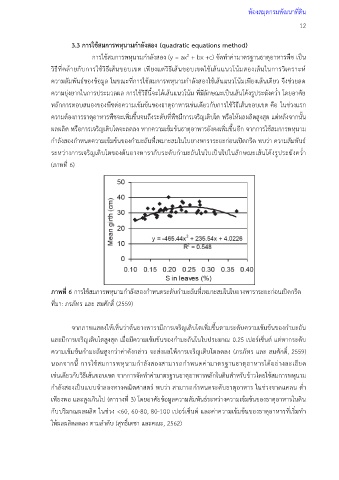
(ภาพที่ 6)
ภาพที่ 6 การใช้สมการพหุนามก้าลังสองก้าหนดระดับก้ามะถันที่เหมาะสมในใบยางพาราระยะก่อนเปิดกรีด
ที่มา: ภรภัทร และ สมศักดิ์ (2559)
จากภาพแสดงให้เห็นว่าต้นยางพารามีการเจริญเติบโตเพิ่มขึ นตามระดับความเข้มข้นของก้ามะถัน
และมีการเจริญเติบโตสูงสุด เมื่อมีความเข้มข้นของก้ามะถันในใบประมาณ 0.25 เปอร์เซ็นต์ แต่หากระดับ
ความเข้มข้นก้ามะถันสูงกว่าค่าดังกล่าว จะส่งผลให้การเจริญเติบโตลดลง (ภรภัทร และ สมศักดิ์, 2559)
นอกจากนี การใช้สมการพหุนามก้าลังสองสามารถก้าหนดค่ามาตรฐานธาตุอาหารได้อย่างละเอียด
เช่นเดียวกับวิธีเส้นขอบเขต จากการจัดท้าค่ามาตรฐานธาตุอาหารหลักในดินส้าหรับข้าวโดยใช้สมการพหุนาม
ก้าลังสองเป็นแบบจ้าลองทางคณิตศาสตร์ พบว่า สามารถก้าหนดระดับธาตุอาหาร ในช่วงขาดแคลน ต่้า
เพียงพอ และสูงเกินไป (ตารางที่ 3) โดยอาศัยข้อมูลความสัมพันธ์ระหว่างความเข้มข้นของธาตุอาหารในดิน
กับปริมาณผลผลิต ในช่วง <60, 60-80, 80-100 เปอร์เซ็นต์ และค่าความเข้มข้นของธาตุอาหารที่เริ่มท้า
ให้ผลผลิตลดลง ตามล้าดับ (สุทธิ์เดชา และคณะ, 2562)